Fall 2020.4 (Schwarz double root) #stuck #complex/qual/completed
Let \(\mathbb{D}:=\{z:|z|<1\}\) denote the open unit disk. Suppose that \(f(z): \mathbb{D} \rightarrow \mathbb{D}\) is holomorphic, and that there exists \(a \in \mathbb{D} \backslash\{0\}\) such that \(f(a)=f(-a)=0\).
-
Prove that \(|f(0)| \leq|a|^{2}\).
-
What can you conclude when \(|f(0)|=|a|^{2} ?\)
Part 1:
Write \(\psi_a(z) \coloneqq{a-z\over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z}\) for the Blaschke factor of \(a\), and define \begin{align*} g(z) \coloneqq{f(z) \over \psi_a(z) \psi_{-a}(z)} .\end{align*}
\({\left\lvert {g(z)} \right\rvert}\leq 1\) on \({\mathbb{D}}\).
\({\left\lvert {\psi_a(z)} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\), so \(\lim_{r\to 1}\psi_a(re^{it}) = 1\) for any fixed \(t\). Then for any \(f\) with \({\left\lvert {f} \right\rvert} \leq 1\) in \({\mathbb{D}}\), \begin{align*} {\left\lvert {f(re^{it} ) \over \psi_a(re^{it} ) } \right\rvert} \leq {1\over \psi_a(re^{it})} \leq {1\over \sup_{t} \psi_a(re^{it}) } \overset{r\to 1}\longrightarrow 1 .\end{align*} So apply this to \(f=g\) and \(f={g\over \psi_a}\) to get it for \({f\over \psi_a \psi_{-a}}.\)
In particular, \({\left\lvert {g(0)} \right\rvert} \leq 1\), so \begin{align*} 1\geq {\left\lvert {g(0)} \right\rvert} = {{\left\lvert {f(0)} \right\rvert} \over {\left\lvert {B_a(0)} \right\rvert} \cdot {\left\lvert {B_{-a}(0)} \right\rvert}} = {{\left\lvert {f(0)} \right\rvert} \over {\left\lvert {a} \right\rvert}^2} \implies {\left\lvert {a} \right\rvert}^2 \geq {\left\lvert {f(0)} \right\rvert} .\end{align*}
Part 2: Applying Schwarz-Pick: \begin{align*} {\left\lvert {f'(0)} \right\rvert} \leq {1 - {\left\lvert {f(0)} \right\rvert}^2 \over 1 - {\left\lvert {0} \right\rvert}^2 } = 1-{\left\lvert {a} \right\rvert}^2 < 1 ,\end{align*} using that \(a\neq 0\), so \(f\) is a contraction.
Can write \(f_e(z) \coloneqq{f(a) + f(-a) \over 2}\) to write \(f_e(z) = g(z^2)\). Compose with some \(\psi_a\) to get \(0\to 0\) and apply Schwarz – unclear how to unwind what happens in the case of equality though.
Fall 2021.5 #complex/qual/completed
Assume \(f\) is an entire function such that \(|f(z)|=1\) on \(|z|=1\). Prove that \(f(z)=e^{i \theta} z^{n}\), where \(\theta\) is a real number and \(n\) a non-negative integer.
Suggestion: First use the maximum and minimum modulus theorem to show \begin{align*} f(z)=e^{i \theta} \prod_{k=1}^{n} \frac{z-z_{k}}{1-\mkern 1.5mu\overline{\mkern-1.5muz_{k}\mkern-1.5mu}\mkern 1.5mu z} \end{align*} if \(f\) has zeros.
First show the hint: assume \(f\) has nonzero zeros. Write \(Z(f) \coloneqq f^{-1}(0)\) for the set of zeros in \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\).
If we assume \(f\) is continuous on \({\mathbb{D}}\), then \({\sharp}Z(f) < \infty\)
Suppose \({\sharp}Z(f) = \infty\), then by compactness of \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) there is a limit point \(z_0\). If \(z_0 \in {\mathbb{D}}\), then there is a sequence \(\left\{{z_k}\right\}\to z_0\) with \(f(z_k) = 0\) for every \(k\), so \(f\) is zero on a set \(S\coloneqq\left\{{z_k}\right\}_{k\geq 1} \cup\left\{{z_0}\right\}\) with an accumulation point and this forces \(f\equiv 0\) on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) by the identity principle, contradicting \({\left\lvert {f} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\)>
Otherwise, if \(z_0\in {{\partial}}{\mathbb{D}}\), using continuity of \(f\) we have \(f(z_k) = 0\) for all \(k\) and \(z_k\to z_0\) so \(f(z_0) = 0\), again contradiicting \({\left\lvert {f} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\).
So write \(Z(f) = \left\{{z_1,\cdots, z_m}\right\}\) and define \begin{align*} g(z) \coloneqq\prod_{1\leq k \leq m} {z-z_k \over 1 - \mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5mu z}, \quad h(z) \coloneqq{f(z) \over g(z)} .\end{align*}
\(h(z) \equiv 1\) is constant on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\), so that \(f = \lambda g\) for some \(\lambda \in S^1\), i.e. \(\lambda = e^{i\theta}\) for some \(\theta\).
Note that \(h\) cancels all zeros of \(f\), so \(h\) is nonzero and holomorphic on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\). Moreover \({\left\lvert {g(z)} \right\rvert} \leq 1\) on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) since these are well-known to be in \(\mathop{\mathrm{Aut}}({\mathbb{D}})\). It’s also well-known that \({\left\lvert {g(z)} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\). Thus \({\left\lvert {h(z)} \right\rvert} = 1\) and \({\left\lvert {1\over h(z)} \right\rvert} =1\) on \({{\partial}}{\mathbb{D}}\), and by the maximum modulus principle, \begin{align*} {\left\lvert {h(z)} \right\rvert} \leq 1 \quad\text{ and }\quad {\left\lvert {1\over h(z)} \right\rvert}\leq 1 \quad \text{ on } {\mathbb{D}} ,\end{align*} forcing \({\left\lvert {h(z)} \right\rvert}\equiv 1\) and thus \(h(z) = e^{i\theta}\) for some \(\theta\).
So we now have \begin{align*} f(z) = e^{i\theta} \prod_{1\leq k\leq m} {z-z_k \over 1 -\mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5mu z} ,\end{align*} which has poles at points \(z\) for which \(\mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5muz=1\) for some \(z_k\in Z(f)\). However, since we assumed \(f\) was entire, it can have no such poles, which forces \(z_k = 0\) for all \(k\). But then \begin{align*} f(z) = e^{i\theta}\prod_{1\leq k \leq m}{z- 0 \over 1 - 0\cdot z} = e^{i\theta}z^m .\end{align*}
Fall 2021.6 (Schwarz manipulation) #complex/qual/completed
Show that if \(f: D(0, R) \rightarrow \mathbb{C}\) is holomorphic, with \(|f(z)| \leq M\) for some \(M>0\), then \begin{align*} \left|\frac{f(z)-f(0)}{M^{2}-\overline{f(0)} f(z)}\right| \leq \frac{|z|}{M R} . \end{align*}
The strategy:
- Write the RHS as \(a\). Note that we need to get rid of the \(M^2\) on the LHS, so keep the \(M\) around and write \(a \coloneqq z/R\) so \(z = aR\).
-
Make the substitution to get
\begin{align*}
{\left\lvert {f(aR) - f(0) \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(aR) } \right\rvert} \leq M^{-1}{\left\lvert {a} \right\rvert} \\
\implies
{\left\lvert {M\qty{ f(aR) - f(0)} \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(aR) } \right\rvert} \leq {\left\lvert {a} \right\rvert} \\
{\left\lvert { f(aR)/M - f(0)/M \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(aR)/M^2 } \right\rvert} \leq {\left\lvert {a} \right\rvert}
.\end{align*}
- Recognize the LHS as \(\psi_w(g(a))\) for \(w\coloneqq f(0)/M\) and \(g(a) \coloneqq f(aR)/M\).
Proof due to Swaroop Hegde!
Fix \(R, M\) and make a clever choice: define \begin{align*} F: {\mathbb{D}}&\to {\mathbb{C}}\\ z &\mapsto {f(Rz) \over M} .\end{align*} Write \(a\coloneqq F(0)\) and consider the Blaschke factor \begin{align*} \psi_a(z) \coloneqq{a-z \over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z} \in \mathop{\mathrm{Aut}}({\mathbb{D}}) ,\end{align*} and define \begin{align*} g: {\mathbb{D}}&\to {\mathbb{D}}\\ z &\mapsto (\psi_a \circ F)(z) .\end{align*} Then \(g(0) = 0\) and \({\left\lvert {g(z)} \right\rvert} \leq 1\) for all \(z\in {\mathbb{D}}\), so by Schwarz we have \({\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}\) for all \(z\in {\mathbb{D}}\). Thus for all \(z\in {\mathbb{D}}\), \begin{align*} &{\left\lvert {g(z)} \right\rvert} \leq z \\ \\ \iff & {\left\lvert {\psi_a(F(z)) } \right\rvert} \leq {\left\lvert {z} \right\rvert} \\ \\ \iff & {\left\lvert { {f(Rz) \over M} - a \over 1 - {\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu f(Rz) \over M} } \right\rvert} \leq {\left\lvert {z} \right\rvert} \\ \\ \iff & {\left\lvert {f(Rz) - f(0) \over 1 - {\mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(Rz) \over M^2 } } \right\rvert} \leq {\left\lvert {z} \right\rvert} \\ \\ \iff & {\left\lvert {f(Rz) - f(0) \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(Rz) } \right\rvert} \leq {{\left\lvert {z} \right\rvert} \over M} \\ \\ \iff & {\left\lvert {f(w) - f(0) \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(w) } \right\rvert} \leq {{\left\lvert {w} \right\rvert} \over MR} ,\end{align*} which holds for all \(w\in {\mathbb{D}}\) by replacing \(Rz\) with \(w\) (i.e. to show this equality for arbitrary \(w\in {\mathbb{D}}\), write \(w = Rz\) for some \(z\in {\mathbb{D}}\) and run this chain of inequalities backward).
Scaling Schwarz #complex/exercise/completed
Let \(\mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu(a, r)\) denote the closed disc of radius \(r\) about \(a\in {\mathbb{C}}\). Let \(f\) be holomorphic on an open set containing \(\mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu(a, r)\) and let \begin{align*} M \coloneqq\sup_{z\in \mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu(a, r)} {\left\lvert {f(z)} \right\rvert} .\end{align*}
Prove that \begin{align*} z\in \mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu\qty{a, {r\over 2}},\,z\neq a, \qquad {{\left\lvert { f(z) - f(a)} \right\rvert} \over {\left\lvert {z-a} \right\rvert}} \leq {2M \over r} .\end{align*}
Set \begin{align*} g(z) \coloneqq{f(Rz+a) - f(a) \over 2M} ,\end{align*} so that \(g(0) = 0\) and \(g:{\mathbb{D}}\to {\mathbb{D}}\) so Schwarz applies, \begin{align*} {\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert} \implies {\left\lvert { f(Rz+a) - f(a) \over 2M } \right\rvert} &\leq {\left\lvert {z} \right\rvert} \\ \implies {\left\lvert { f(Rz+a) - f(a) } \right\rvert} &\leq 2M {\left\lvert {z} \right\rvert} \\ \implies {\left\lvert { f(w) - f(a) } \right\rvert} &\leq 2M{\left\lvert { w-a\over R} \right\rvert} \\ \implies {\left\lvert {f(w) - f(a) \over w-a} \right\rvert} &\leq {2M \over R} .\end{align*}
Bounding derivatives #complex/exercise/completed
Suppose \(f: {\mathbb{D}}\to {\mathbb{H}}\) is analytic and satisfies \(f(0) = 2\). Find a sharp upper bound for \({\left\lvert {f'(0)} \right\rvert}\), and prove it is sharp by example.
Some useful facts about the Cayley map:
- \(C(z) \coloneqq{z-i\over z+i}\) maps \({\mathbb{H}}\to {\mathbb{D}}\) sending \(i\to 0\).
- \(C^{-1}(z) \coloneqq-i {z+1\over z-1}\) maps \({\mathbb{D}}\to{\mathbb{H}}\) sending \(0\to i\).
- \(C'(z) = {2i\over (z+i)^2}\) and \(C'(i) = -{1\over 2}i\).
- \((C^{-1})'(z) = {2i\over (z-1)^2}\) and \(C'(0) = 2i\).
- A mistake that’s useful to know: \(\psi_w'(z) = {1-{\left\lvert {w} \right\rvert}^2 \over (1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5muz )^2}\) and \(\psi_w'(w) \to \infty\).
Define \(g:{\mathbb{H}}\to {\mathbb{H}}\) by \(g(z) = {1\over 2}iz\), so \(g(2) = i\). Then set \(F \coloneqq C\circ g \circ f: {\mathbb{D}}\to {\mathbb{D}}\) where \(C(z) \coloneqq{z-i\over z+i}\) is the Cayley map.Since \(F(0) = C(g(f(0))) = C(g(2)) = C(i) = 0\), Schwarz applies to \(F\) and \({\left\lvert {F'(z)} \right\rvert}\leq 1\) for \(z\in {\mathbb{D}}\). By the chain rule, \begin{align*} F'(z) = f'( (g\circ C) (z))\cdot g'(C(z)) \cdot C'(z) .\end{align*} Setting \(g(C(z)) = 0\) yields \(z=C^{-1}(g^{-1}(0)) = C^{-1}(0) = i\). \begin{align*} F'(i) &= f'(0) \cdot g'(0) \cdot C'(i) \\ \implies {\left\lvert {f'(0)} \right\rvert} &\leq {\left\lvert {F'(i) \over g'(0) C'(i)} \right\rvert} \\ &\leq {1\over {\left\lvert {g'(0)} \right\rvert} \cdot {\left\lvert {C'(i)} \right\rvert} } \\ &= {1\over {\left\lvert {i\over 2} \right\rvert} \cdot {\left\lvert {-{i\over 2} } \right\rvert} } \\ &= 4 .\end{align*}
By Schwarz, if \({\left\lvert {F'(z)} \right\rvert} = 1\) for any \(z\in {\mathbb{D}}\), we’ll have \(F(z) = \lambda z\) for some \({\left\lvert { \lambda} \right\rvert} = 1\). Unwinding this: \begin{align*} F(z) &= \lambda z \implies (C\circ g\circ f)(z) = \lambda z \\ \implies f(z) &= g^{-1}(C^{-1}(\lambda z)) = g^{-1}\qty{-i {\lambda z + 1 \over \lambda z - 1}} \\ \implies f(z) &= -2 {\lambda z + 1\over \lambda z - 1} .\end{align*} Moreover \(f'(z) = -2\qty{-2\lambda \over (\lambda z - 1)^2}\), so \begin{align*} {\left\lvert {f'(0)} \right\rvert} = 4{\left\lvert {\lambda} \right\rvert} = 4 .\end{align*}
Schwarz for higher order zeros #complex/exercise/completed
Suppose \(f:{\mathbb{D}}\to{\mathbb{D}}\) is analytic, has a single zero of order \(k\) at \(z=0\), and satisfies \(\lim_{{\left\lvert {z} \right\rvert} \to 1} {\left\lvert {f(z)} \right\rvert} = 1\). Give with proof a formula for \(f(z)\).
Note \({\left\lvert {f(z)} \right\rvert}\leq 1\), and \(g\coloneqq f(z)/z^k\) has a removable singularity at zero since \(g\) is bounded on \({\mathbb{D}}\): fixing \({\left\lvert {z} \right\rvert} = r < 1\), \begin{align*} {\left\lvert {g(z)} \right\rvert} = {\left\lvert {f(z)\over z^k} \right\rvert} = {\left\lvert {f(z)} \right\rvert}r^{-k}\leq r^{-k}\overset{r\to 1}\longrightarrow 1 .\end{align*} So \(g:{\mathbb{D}}\to {\mathbb{D}}\) since \({\left\lvert {g(z)} \right\rvert}\leq 1\) on \({\mathbb{D}}\) by the MMP. Since \(g\) has no zeros on \({\mathbb{D}}\), by the MMP \({\left\lvert {g} \right\rvert} \geq 1\) on \({\mathbb{D}}\), so \({\left\lvert {g} \right\rvert} = 1\) is constant, making \(g(z) = \lambda z\) a rotation. Then \(f(z) = \lambda z^n\).
Alternative to MMP: if \(g\) has no zeros in \({\mathbb{D}}\), \(g\) admits a conjugate reflection through \({\mathbb{D}}\) by \(z\mapsto 1/\mkern 1.5mu\overline{\mkern-1.5muf(1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\). This is bounded and entire, thus constant, making \(g\) constant.
Schwarz with an injective function #complex/exercise/completed
Suppose \(f, g: {\mathbb{D}}\to \Omega\) are holomorphic with \(f\) injective and \(f(0) = g(0)\).
Show that \begin{align*} \mathop{\mathrm{\forall}}0 < r < 1,\qquad g\qty{\left\{{{\left\lvert {z} \right\rvert} < r}\right\}} \subseteq f\qty{\left\{{{\left\lvert {z} \right\rvert} < r}\right\}} .\end{align*}
The first part of this problem asks for a statement of the Schwarz lemma.
Since \(f\) is injective, it has a left-inverse \(f^{-1}\), and \(F\coloneqq f^{-1}g\) is well-defined. Since \(F:{\mathbb{D}}\to {\mathbb{D}}\) and \(F(0) = 0\), Schwarz applies and \({\left\lvert {F(z)} \right\rvert} \leq z\) on \({\mathbb{D}}\). Unwinding: \begin{align*} {\left\lvert {(f^{-1}\circ g)(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert} \implies {\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {f(z)} \right\rvert} \qquad \forall {\mathbb{D}}\in {\mathbb{Z}} .\end{align*} This says that \(g({\mathbb{D}}) \subseteq f({\mathbb{D}})\), and in particular this holds on all \({\mathbb{D}}_r(0)\), so \(g({\mathbb{D}}_r(0)) \subseteq f({\mathbb{D}}_r(0))\).
Reflection principle #complex/exercise/completed
Let \(S\coloneqq\left\{{z\in {\mathbb{D}}{~\mathrel{\Big\vert}~}\Im(z) \geq 0}\right\}\). Suppose \(f:S\to {\mathbb{C}}\) is continuous on \(S\), real on \(S\cap{\mathbb{R}}\), and holomorphic on \(S^\circ\).
Prove that \(f\) is the restriction of a holomorphic function on \({\mathbb{D}}\).
Define a function \begin{align*} F(z) \coloneqq \begin{cases} f(z) & \Im(z)\geq 0 \\ \mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu & \Im(z) < 0 \end{cases} .\end{align*} Then \(F\) is holomorphic on \(\tilde S\coloneqq\left\{{z\in {\mathbb{D}}{~\mathrel{\Big\vert}~}\Im(z) < 0}\right\}\) – write \(w_0\in \tilde S\) as \(w_0 = \mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu\) for some \(z_0\in S\), then \begin{align*} f(z) &= \sum_{k\geq 0}c_k (z-z_0)^k \\ \implies \mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu &= \sum_{k\geq 0}\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \mkern 1.5mu\overline{\mkern-1.5mu\qty{\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - z_0}^k\mkern-1.5mu}\mkern 1.5mu \\ &= \sum_{k\geq 0}\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \qty{z - \mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu}^k \\ &= \sum_{k\geq 0}\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \qty{z - w_0}^k ,\end{align*} which yields a power series expansion of \(F\) about \(w_0\). So \(f\) is analytic at every point in \(\tilde S\) and thus holomorphic. Since \(\mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu = f(z)\) for \(z, f(z)\in {\mathbb{R}}\), \(F\) is a continuous extension of \(f\) to \({\mathbb{D}}\). By the symmetry principle, \(F\) is holomorphic, and \({ \left.{{F}} \right|_{{S}} } = f\).
Blaschke Factors
Spring 2019.5, Spring 2021.5 (Blaschke contraction) #complex/qual/completed
Let \(f\) be a holomorphic map of the open unit disc \({\mathbb{D}}\) to itself. Show that for any \(z, w\in {\mathbb{D}}\), \begin{align*} \left|\frac{f(w)-f(z)}{1-\overline{f(w)} f(z)}\right| \leq\left|\frac{w-z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\right| .\end{align*} Show that this inequality is strict for \(z\neq w\) except when \(f\) is a linear fractional transformation from \({\mathbb{D}}\) to itself.
The Schwarz conjugation trick:
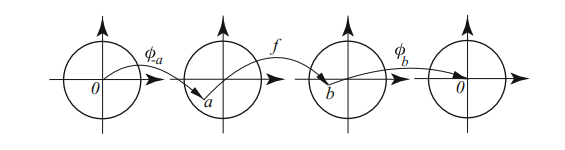
Write the RHS as \(a\), we then want something in the form \({\left\lvert {F(a)} \right\rvert}\leq {\left\lvert {a} \right\rvert}\). The choice \(a=\psi_w(z)\) is forced, so \(z= \psi_w^{-1}(a)\). This forces the choice for the LHS \begin{align*} { f(w) - (f\circ \psi_w^{-1})(a) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5mu (f\circ \psi_w^{-1})(a) } = (\psi_{f(w)} \circ f \circ \psi_w^{-1})(a) \coloneqq F(a) .\end{align*}
This is the Schwarz–Pick lemma.
-
Fix \(z_1\) and let \(w_1 = f(z_1)\). Define \begin{align*} \psi_{a}(z) \coloneqq{a-z \over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5muz} \in \mathop{\mathrm{Aut}}({\mathbb{D}}) .\end{align*}
- Note that inequality now reads \begin{align*} {\left\lvert {\psi_{f(w)}(f(z)) } \right\rvert} \leq {\left\lvert {\psi_w(z)} \right\rvert} .\end{align*} Moreover \(\psi_a\) is an involution that swaps \(a\) and \(0\).
-
Now set up a situation where Schwarz’s lemma will apply: \begin{align*} 0 \xrightarrow{\psi_{z_1}} z_1 \xrightarrow{f} f(z) \xrightarrow{\psi_{f(z_1)}} 0 ,\end{align*} so \(F\coloneqq\psi_{f(z_1)} \circ f \circ \psi_{z_1} \in \mathop{\mathrm{Aut}}({\mathbb{D}})\) and \(F(0) = 0\).
-
Apply Schwarz we get \({\left\lvert {F(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}\) for all \(z\), so \begin{align*} {\left\lvert {F(z)} \right\rvert} &\leq {\left\lvert {z} \right\rvert} \\ \implies {\left\lvert { f(z_1) - (f\circ \psi_{z_1})(z) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(z_1)\mkern-1.5mu}\mkern 1.5mu \cdot (f\circ \psi_{z_1}) (z) } \right\rvert} &\leq {\left\lvert { z} \right\rvert} \\ \implies {\left\lvert {f(z_1) - f(w) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(z_1)\mkern-1.5mu}\mkern 1.5mu\cdot f(w) } \right\rvert} &\leq {\left\lvert {\psi_{z_1}(z)} \right\rvert} && w\coloneqq\psi_{z_1}(z) \\ \implies {\left\lvert {f(z_1) - f(w) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(z_1)\mkern-1.5mu}\mkern 1.5mu\cdot f(w) } \right\rvert} &\leq {\left\lvert {z_1 - z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muz_1\mkern-1.5mu}\mkern 1.5mu z } \right\rvert} .\end{align*}
-
Since \(z_1\) was arbitrary and fixed and \(w\) was a free variable, this holds for all \(z,w\in {\mathbb{D}}\).
-
Strictness: suppose equality holds, we’ll show that \(f(z) = {az+b\over cz+d}\)
-
By Schwarz, \(F(z) = \lambda z\) for \(\lambda \in S^1\). Thus \begin{align*} (\psi_{f(z_1)} \circ f \circ \psi_{z_1}) (z) &= \lambda z \\ \implies (f \circ \psi_{z_1}) (z) &= \psi_{f(z_1)}^{-1}(\lambda z ) \\ \implies f(w) &= \psi_{f(z_1)}^{-1}(\lambda \psi_{z_1}^{-1}(w) ) && w\coloneqq\psi_{z_1}(z) \\ &= \psi_{f(z_1)} \qty{\lambda \psi_{z_1}(w)} \\ &= \lambda \psi_{\mkern 1.5mu\overline{\mkern-1.5mu\lambda \mkern-1.5mu}\mkern 1.5muf(z_1)} \qty{\psi_{z_1}(w)} \\ &\coloneqq\lambda \psi_a(\psi_b(w)) \\ &=\lambda\qty{ a- \psi_b(w) \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu \psi_b(w) } \\ &= \quad \vdots \\ &= -\lambda \qty{ \frac{{\left(a \overline{b} - 1\right)} z - a + b}{{\left(\overline{a} - \overline{b}\right)}z - b \overline{a} + 1} } \\ &= \qty{ \frac{-\lambda {\left(a \overline{b} - 1\right)} z + \lambda( a - b)}{{\left(\overline{a} - \overline{b}\right)}z + (- b \overline{a} + 1)} } ,\end{align*} which is evidently a linear fractional transformation.
Schwarz-Pick derivative #complex/exercise/completed
Suppose \(f:{\mathbb{D}}\to {\mathbb{D}}\) is analytic. Prove that \begin{align*} \forall a\in {\mathbb{D}}, \qquad {{\left\lvert {f'(a)} \right\rvert} \over 1 - {\left\lvert {f(a)} \right\rvert}^2 } \leq {1 \over 1 - {\left\lvert {a} \right\rvert}^2} .\end{align*}
Holomorphic maps on \({\mathbb{D}}\) contract Blaschke factors: \begin{align*} {\left\lvert { \psi_w(z) } \right\rvert} \geq {\left\lvert {\psi_{f(w)}(f(z)) } \right\rvert} ,\end{align*} i.e. \begin{align*} {\left\lvert {f(w) - f(z) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5muf(z)} \right\rvert} \leq {\left\lvert {w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} .\end{align*}
Make a change of variables \(a\coloneqq\psi_w(z)\) so \(z=\psi_w^{-1}(a) = \psi_w(a)\), then the desired inequality follows if we can show \begin{align*} {\left\lvert { \psi_{f(w)}(f(\psi_w(a))) } \right\rvert} \leq {\left\lvert {a} \right\rvert} .\end{align*}
So define \(F \coloneqq\psi_{f(w)} \circ f \circ \psi_w\), then since \(\psi_w(0) = w\), \begin{align*} F(0) = \psi_{f(w)}(f(w)) = 0 .\end{align*} Moreover \({\left\lvert {F(z)} \right\rvert}\leq 1\) since each constituent is a map \({\mathbb{D}}\to {\mathbb{D}}\). So \(F\) satisfies Schwarz and the claim follows.
Given this, there’s just a clever rearrangement to obtain the stated result: \begin{align*} {\left\lvert {f(w) - f(z) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5muf(z)} \right\rvert} &\leq {\left\lvert {w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} \\ \implies {\left\lvert { 1\over 1-\mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5muf(z) } \right\rvert} \cdot {\left\lvert {f(z) - f(w) \over z-w} \right\rvert} &\leq {\left\lvert {1\over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5muz} \right\rvert} \\ ,\end{align*} and taking \(z\to w\) on both sides yields \begin{align*} {\left\lvert {1\over 1 - {\left\lvert {f(w)} \right\rvert}^2 } \right\rvert} {\left\lvert {f'(w)} \right\rvert} \leq {1\over {\left\lvert {w} \right\rvert}^2} \implies {\left\lvert {f'(w)} \right\rvert} \leq {1-{\left\lvert {f(w)} \right\rvert}^2\over 1-{\left\lvert {w} \right\rvert}^2 } .\end{align*}
Schwarz and Blaschke products #complex/exercise/completed
Suppose \(f:{\mathbb{D}}\to{\mathbb{D}}\) is analytic and admits a continuous extension \(\tilde f: \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\to \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) such that \({\left\lvert {z} \right\rvert} = 1 \implies {\left\lvert {f(z)} \right\rvert} = 1\).
-
Prove that \(f\) is a rational function.
-
Suppose that \(z=0\) is the unique zero of \(f\). Show that \begin{align*} \exists n\in {\mathbb{N}}, \lambda \in S^1 {\quad \operatorname{ such that } \quad}f(z) = \lambda z^n .\end{align*}
- Suppose that \(a_1, \cdots, a_n \in {\mathbb{D}}\) are the zeros of \(f\) and prove that \begin{align*} \exists \lambda \in S^1 {\quad \operatorname{such that} \quad} f(z) = \lambda \prod_{j=1}^n {z - a_j \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua_j\mkern-1.5mu}\mkern 1.5mu z} .\end{align*}
Part 1: use the reflection principle to define \begin{align*} F(z) \coloneqq \begin{cases} f(z) & {\left\lvert {z} \right\rvert} \leq 1 \\ {1\over \mkern 1.5mu\overline{\mkern-1.5muf\qty{1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu}\mkern-1.5mu}\mkern 1.5mu } & {\left\lvert {z} \right\rvert} \geq 1 \end{cases} .\end{align*}
Now \(F:{\mathbb{CP}}^1\to {\mathbb{CP}}^1\) is holomorphic and all such functions are rational. As a consequence, \(f\) is rational.
Part 2: As in the proof of Schwarz, define \(g(z) \coloneqq{f(z)\over z^n}\) where \(n = {\operatorname{Ord}}_{f}(0)\). Then \(g\) is holomorphic on \({\mathbb{D}}\) since the singularity at \(z=0\) is removable. On \({\left\lvert {z} \right\rvert} = r<1\), \begin{align*} {\left\lvert {g(z)} \right\rvert} = { {\left\lvert {f(z)} \right\rvert} \over {\left\lvert {z} \right\rvert} } = {{\left\lvert {f(z)} \right\rvert} \over r} \leq {1\over r} \overset{r\to 1^-}\longrightarrow 1 ,\end{align*} using that \({\left\lvert {f} \right\rvert} \leq 1\) on \({\mathbb{D}}\). By the MMP, \({\left\lvert {g} \right\rvert} \leq 1\) on all of \({\mathbb{D}}\). Note that \({\left\lvert {g} \right\rvert} = 1\) when \({\left\lvert {z} \right\rvert}=1\), so \({\left\lvert {1/g} \right\rvert}\leq 1\) in \({\mathbb{D}}\) by the MMP, forcing \({\left\lvert {g} \right\rvert} = 1\). Unwinding this, \({\left\lvert {f} \right\rvert} = {\left\lvert {z} \right\rvert}^n\), go \(f(z) = \lambda z^n\) for some \({\left\lvert {\lambda} \right\rvert} = 1\).
Part 3: Define \(\Psi(z) \coloneqq\prod_{k\leq n} \psi_{a_k}(z)\) where \(\psi_a(z) \coloneqq{a-z\over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z}\). Set \(g(z) \coloneqq{f(z) \over \Psi(z)}\), then by the same argument as above, \({\left\lvert {g} \right\rvert} \leq 1\) and \({\left\lvert {g} \right\rvert} = 1\) on \({\left\lvert {z} \right\rvert} = 1\). Then \(g\) has no zeros, since they’ve all been divided out, and no poles since \(f\) is holomorphic on \({\mathbb{D}}\), so \(1/g\) is holomorphic on \({\mathbb{D}}\). Since \({\left\lvert {1/g} \right\rvert} = 1\) on \(S^1\), this forces \(g\) to be constant. Equality in the Schwarz lemma implies \(g(z) = \lambda z\) is a rotation, and unwinding this yields \(f(z) = \lambda \Psi(z)\).
Tie’s Extra Questions: Fall 2009 #complex/exercise/completed
Let \(g\) be analytic for \(|z|\leq 1\) and \(|g(z)| < 1\) for \(|z| = 1\).
-
Show that \(g\) has a unique fixed point in \(|z| < 1\).
-
What happens if we replace \(|g(z)| < 1\) with \(|g(z)|\leq 1\) for \(|z|=1\)? Give an example if (a) is not true or give an proof if (a) is still true.
-
What happens if we simply assume that \(f\) is analytic for \(|z| < 1\) and \(|f(z)| < 1\) for \(|z| < 1\)? Suppose that \(f(z) \not\equiv z\). Can f have more than one fixed point in \(|z| < 1\)?
Hint: The map \(\displaystyle{\psi_{\alpha}(z)=\frac{\alpha-z}{1-\mkern 1.5mu\overline{\mkern-1.5mu\alpha\mkern-1.5mu}\mkern 1.5muz}}\) may be useful.
Use Rouché: if \({\left\lvert {f(z)} \right\rvert} < 1\) is strict when \({\left\lvert {z} \right\rvert} = 1\), then consider \(F(z) \coloneqq f(z) - z\). Write the big part as \(M(z) = z\) and the small as \(m(z) = f(z)\), then on \({\left\lvert {z} \right\rvert} = 1\) \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {f(z)} \right\rvert} < 1 = {\left\lvert {z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(M(z)\) and \(m(z) + M(z) = f(z) - z\) have the same number of zeros in \({\mathbb{D}}\) – precisely one.
There is still a unique fixed point. Use the Brouwer fixed point theorem: since \(g\) is holomorphic on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\), it is in particular continuous. By the Brouwer fixed point theorem, every continuous map \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu \to \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) has a fixed point. If \(g\) is nonconstant, then the fixed point is unique by Schwarz: without loss of generality one can assume \(f(0) = 0\) by composing with a Blaschke factor. Apply Schwarz to \(f\), then if \(f(a) = a\) we have the equality clause and \(f(z) = \lambda z\). Since \(a = f(a) = \lambda a\), \(\lambda = 1\) and \(f\) is the identity. If \(g\) is constant, then \({\left\lvert {g(z)} \right\rvert} < 1\) on \({\left\lvert {z} \right\rvert} = 1\) forces \(g\equiv 0\).
Note that there is a major difference between self maps to \({\mathbb{D}}\) versus \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\). By the argument in part 2, if \(f(z)\) is not the identity then \(f\) can have at most one fixed point. Moreover, not every map \(f:{\mathbb{D}}\to{\mathbb{D}}\) need have a fixed point: consider \begin{align*} g: {\mathbb{H}}&\to {\mathbb{H}}\\ z &\mapsto z+1 .\end{align*} Now conjugate with the Cayley map \(C:{\mathbb{H}}\to {\mathbb{D}}\) to define \(f\coloneqq CgC^{-1}:{\mathbb{D}}\to {\mathbb{D}}\) which has no fixed points at all.
Tie’s Extra Questions: Fall 2015 (Blaschke factor properties) #complex/exercises/completed
-
Let \(z, w\) be complex numbers, such that \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \neq 1\). Prove that \begin{align*}{\left\lvert {\frac{w - z}{1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}} \right\rvert} < 1 \; \; \; \mbox{if} \; |z| < 1 \; \mbox{and}\; |w| < 1,\end{align*} and also that \begin{align*}{\left\lvert {\frac{w - z}{1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}} \right\rvert} = 1 \; \; \; \mbox{if} \; |z| = 1 \; \mbox{or}\; |w| = 1.\end{align*}
-
Prove that for fixed \(w\) in the unit disk \(\mathbb D\), the mapping \begin{align*}F: z \mapsto \frac{w - z}{1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\end{align*} satisfies the following conditions:
-
\(F\) maps \(\mathbb D\) to itself and is holomorphic.
-
\(F\) interchanges \(0\) and \(w\), namely, \(F(0) = w\) and \(F(w) = 0\).
-
\({\left\lvert {F(z)} \right\rvert} = 1\) if \(|z| = 1\).
-
\(F: {\mathbb D} \mapsto {\mathbb D}\) is bijective.
-
Hint: Calculate \(F \circ F\).
Tie’s Extra Questions: Spring 2015 #complex/exercise/completed
Suppose \(f\) is analytic in an open set containing the unit disc \(\mathbb D\) and \(|f(z)| =1\) when \(|z|\)=1. Show that either \(f(z) = e^{i \theta}\) for some \(\theta \in \mathbb R\) or there are finite number of \(z_k \in \mathbb D\), \(k \leq n\) and \(\theta \in \mathbb R\) such that \begin{align*} \displaystyle f(z) = e^{i\theta} \prod_{k=1}^n \frac{z-z_k}{1 - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_k z } \, . .\end{align*}
Also cf. Stein et al, 1.4.7, 3.8.17
Tie’s Extra Questions: Spring 2015 (Equality of modulus) #complex/exercise/completed
Let \(f\) and \(g\) be non-zero analytic functions on a region \(\Omega\). Assume \(|f(z)| = |g(z)|\) for all \(z\) in \(\Omega\). Show that \(f(z) = e^{i \theta} g(z)\) in \(\Omega\) for some \(0 \leq \theta < 2 \pi\).
Define \(F(z) \coloneqq{f(z) \over g(z)}\).
\(F\) is holomorphic on \(\Omega\).
Note that \(g(a) = 0\) iff \(f(a) = 0\), so \(F\) has no poles. If \(F\) has a singularity at \(z_0\), noting that \({\left\lvert {F(z_0)} \right\rvert} = 1\), \(F\) is bounded in a neighborhood of \(z_0\) and thus the singularity must be removable. By Riemann’s removable singularity theorem, \(F\) extends to a holomorphic function.
Given this, note that \({\left\lvert {F(z)} \right\rvert} = 1\) for all \(z\), so \(F(\Omega) \subseteq S^1\), which is codimension 1 in \({\mathbb{C}}\) and not open. By the open mapping theorem, \(F\) must be constant, so \(F(z) = \lambda\), and in particular since \({\left\lvert {F(z)} \right\rvert} = 1\), \(\lambda = e^{it}\in S^1\) for some \(t\). Then \(f(z) = \lambda g(z)\).
Fixed Points
Fall 2020.7 #complex/qual/completed
Suppose that \(f: \mathbb{D} \rightarrow \mathbb{D}\) is holomorphic and \(f(0)=0\). Let \(n \geq 1\), and define the function \(f_{n}(z)\) to be the \(n\)-th composition of \(f\) with itself; more precisely, let
\begin{align*} f_{1}(z):=f(z), f_{2}(z):=f(f(z)), \text { in general } f_{n}(z):=f\left(f_{n-1}(z)\right) . \end{align*}
Suppose that for each \(z \in \mathbb{D}, \lim _{n \rightarrow \infty} f_{n}(z)\) exists and equals to \(g(z)\). Prove that either \(g(z) \equiv 0\) or \(g(z)=z\) for all \(z \in D\).
Note that there is a unique fixed point. We have \(f(0) = 0\), so there is at least one, so suppose \(a\) is another fixed point with \(f(a) = a\). By Schwarz, \({\left\lvert {f(z)} \right\rvert}\leq {\left\lvert {z} \right\rvert}\) with equality at any nonzero point implying \(f\) is a rotation, and \(f(a) = a\implies {\left\lvert {f(a)} \right\rvert} = {\left\lvert {a} \right\rvert}\), so write \(f(z) = e^{i\theta}z\). Now \(f(a) = a = e^{i\theta }a\) forces \(\theta = 0\), so \(f(z) = z\) is the identity.
Since \(f(0) = 0\), the Schwarz lemma applies and either
- \(f(z) = e^{i\theta} z\) is a rotation, or
- \({\left\lvert {f'(0)} \right\rvert} < 1\) and \({\left\lvert {f(z)} \right\rvert} < z\) for all \(z\in {\mathbb{D}}\).
Supposing the latter, \(f\) is a contraction, and \({\left\lvert {f_{n+1}(z)} \right\rvert} < {\left\lvert {f_{n}(z)} \right\rvert}\) for all \(n\) and all \(z\), so \({\left\lvert {f_n(z)} \right\rvert} \overset{n\to\infty}\longrightarrow 0\) for all \(z\). Since \(f_n\to g\) pointwise, this means \(g(z) = 0\) for all \(z\), making \(g\equiv 0\).
Otherwise, suppose \(f\) is a rotation. Then if \(f(z) = e^{i\theta}z\), \(f_n(z) = e^{in\theta}z\). The pointwise limit \(\lim_{n\to\infty}e^{in\theta}z\) can only exist if \(\theta = 0\), otherwise this is periodic when \(\theta\) is rational or the points \(e^{i\theta}z, e^{2i\theta }z,\cdots\) form form a countably infinite set of distinct points. So \(f(z) = z\), making \(\lim_{n\to \infty}f_n(z) = z\) as well.